Das deutsche Python-Forum

Moin Zusammen,
gibt es eine effiziente Methode um gleitend zu integrieren?

Was ich meine ist bspw. die Integration eines Beschleunigungsarrays zu einem Geschwindigkeitsarrays
Ich kann mir natürlich eine Schleife schreiben, was aber performancetechnisch bei samples >100k völlig inakzeptabel wäre...

Besten Dank!
Squipy

Benutz numpy. Dann geht das schnell.

Das hört sich ja vielversprechend an. Ich habe leider trotzdem insbesondere bei numpy noch keine Möglichkeit der numerischen Integration gefunden. Z.B gibt es das:

Code: Alles auswählen

acc = [20, -10, 5, -25, 60, -70, 10]
v = np.trapz(acc,dx =1)

Das ist aber leider nicht das was ich suche, weil das gesamte Signale integriert wird und mir dan ngenau einen wert ausspuckt.

Ich verstehe nicht was du meinst. Wieviele Werte willst du denn haben?

In der Messtechnik kann es interessant sein, neben der Schwingbeschleunigung die Schwingschnelle zu betrachten. Um das zu erhalten wäre es denkbar das Signal numerisch zu integrieren. In diesem Fall mit konstanter sampling rate könnte das wie folgt realisiert werden:

Code: Alles auswählen

acc = [20, -10, 5, -25, 60, -70, 10]
v = []
dx = 1
v_value = 0
for i in range(0,len(acc)):
    v_value += (acc[i+1]-acc[i])*dx
    v.append(v_value)

Das ist aber leider bei Messwerten >100k sehr langwierig. Meine Frage ist, ob es dazu eine effiziente Methode gibt. Am schönsten wäre natürlich mit trapezregel.
Danke und Gruß

Ohne Trapezregel geht’s zb mit https://docs.scipy.org/doc/numpy/refere ... mpy.cumsum

Bei der cumsum funktion kommt leider etwas merkwürdiges raus

Code: Alles auswählen

integral_cumsum = np.cumsum(acc)


def integrate_square(x,dx):
    int_value = 0
    integral =[]
    for i in range(0,len(x)):
        int_value += (x[i-1]-x[i])*dx
        integral.append(int_value)
    return integral

integral_def = integrate_square(acc,dx)

fig, axs = plt.subplots(2)
axs[0].plot(integral_def)
axs[0].set_title("Integration with loop")
axs[1].plot(integral_cumsum)
axs[1].set_title("Cumsum method")

Hast du mal die roh Daten?

Wenn ich folgendes Skript laufen lasse

Code: Alles auswählen

 import numpy as np
import matplotlib.pyplot as plt

acc = np.linspace(0, 100)
integral_cumsum = np.cumsum(acc)


def integrate_square(x,dx):
    int_value = 0
    integral =[]
    for i in range(0,len(x)):
        int_value += (x[i-1]-x[i])*dx
        integral.append(int_value)
    return integral

dx = 1
integral_def = integrate_square(acc,dx)

fig, axs = plt.subplots(2)
axs[0].plot(integral_def)
axs[0].set_title("Integration with loop")
axs[1].plot(integral_cumsum)
axs[1].set_title("Cumsum method")
plt.show()

dann sieht das Ergebnis für cumsum genau so aus, wie ich das erwarten wurde. Anders als dein Code.

Bild

Ich habe mir nochmal deinen Algorithmus angeschaut. IMHO ist deine Trapezfunktion falsch. Du musst die beiden Werte addieren, und dann durch zwei dividieren. Und dann natürlich mit der Schrittweite multiplizieren. Dadurch bekommst du das Trapez. Dann sieht der Graf für mich auch fast gleich aus - da ist ein of-by-one Fehler irgendwo, cumsum liefert am Anfang ein 0 oder so.

ja da hast du recht. Ich denke ich habe jetzt auch den Denkfehler gefunden... Um ein Beschleunigungssignal zu integrieren, wird die Beschleunigungsänderung benötigt und diese muss dann mit delta t multipliziert werdne. Ich habe mal meine paint skills spielen lassen um das zu veranschaulichen. Zumindest vermute ich, dass da der Unterschied besteht.

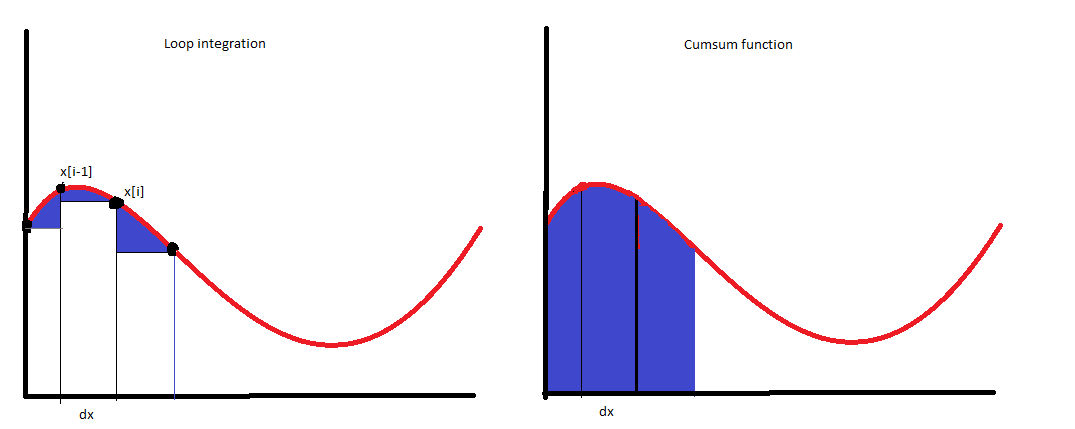
Das Ergebnis der integration eines schwingenden Signals um 0 muss ebenfalls ein schwingendes Signal um 0 ergeben, dementsprechend liefert die loop funktion schon die richtigen Werte (bis auf den ersten Wert, der sollte 0 sein, wie du schon sagtest)

Nein. Da hast du einen Denkfehler. Was du da berechnest (Links) ist die ABLEITUNG deines Signals, nämlich die Differenz der aufeinander folgenden Schritte. Und die integrierst du dann, wobei natürlich im Grunde nix anderes als das ursprüngliche Signal rauskommt. Modulo einer Konstanten C und Rundungsfehlern. Also mitnichten die Geschwindigkeit.

Das rechte Bild ist falsch bezüglich deiner Beschreibung: ein schwingendes Signal um 0. Damit hätten die Balken periodisch auch negative Vorzeichen. Haben sie aber bei dir nicht. Nimm mal mein Beispiel und ersetz die Zeile die ich zur Simulation von acc gebaut habe mit

acc = np.sin(np.linspace(0, 100, num=1000))

Da hast du dann dein wirklich periodisches Signal schwingend um 0. Und cumsum liefert dann den erwarten Phasenverschub, denn das Integral von Sinus ist ja -cos.

Ich habe nochmal etwas mit deinem Code gespielt, und dabei ist mir noch mehr aufgefallen. Du hast einen Vorzeichenfehler. Du berechnest x0 - x1, x1 - x2, ... Doch du musst x1 - x0, x2 - x1, ... rechnen. Und noch einen Index-Fehler, der mit meinem Datensatz verwirrend war. Ich habe das mal unten einfach durch -= korrigiert. Auf dem iPad ist editieren doof. Wenn du das laufen lässt siehst du, das ich recht habe: dein ding integriert die Ableitung, und erzeugt nur wieder die Ursprungsdaten.

Code: Alles auswählen

import numpy as np
import matplotlib.pyplot as plt

acc = np.linspace(0, 100)
integral_cumsum = np.cumsum(acc)


def integrate_square(x,dx):
    int_value = 0
    integral =[]
    for i in range(1,len(x)):
        #print(i, int_value)
        int_value -= (x[i-1]-x[i])*dx
        integral.append(int_value)
    return integral

dx = 1
integral_def = integrate_square(acc,dx)

fig, axs = plt.subplots(3)
axs[0].plot(integral_def)
axs[0].set_title("Integration with loop")
axs[1].plot(integral_cumsum)
axs[1].set_title("Cumsum method")
axs[2].plot(acc)
axs[2].set_title("acc")
plt.show()

Hi _desh_,

du hast vollkommen recht und ich habe mittlerweile auch die Ursache für die aufsteigende Flanke die die cumsum funktion ausspuckt. Das Problem ist, dass das Beschleunigungssignal einen Offset besitzt und dieser dementsprechend mitintegriert und nach jedem step aufsummiert wird.
Es gibt nun verschieden Möglichkeiten diesen Offset zu ignorieren

Davon ausgehen, dass der Offset immer gleich ist und das arithmetische mittel vorher abziehen

Offsetelimination mittels Hochpassfilter

Integration des Spektrums

Wobei der letzt genannte Punkt wohl am genausten ist, dennoch habe ich die ersten beiden Varianten mal versucht und das sieht dann auch schon wesentlich besser aus:

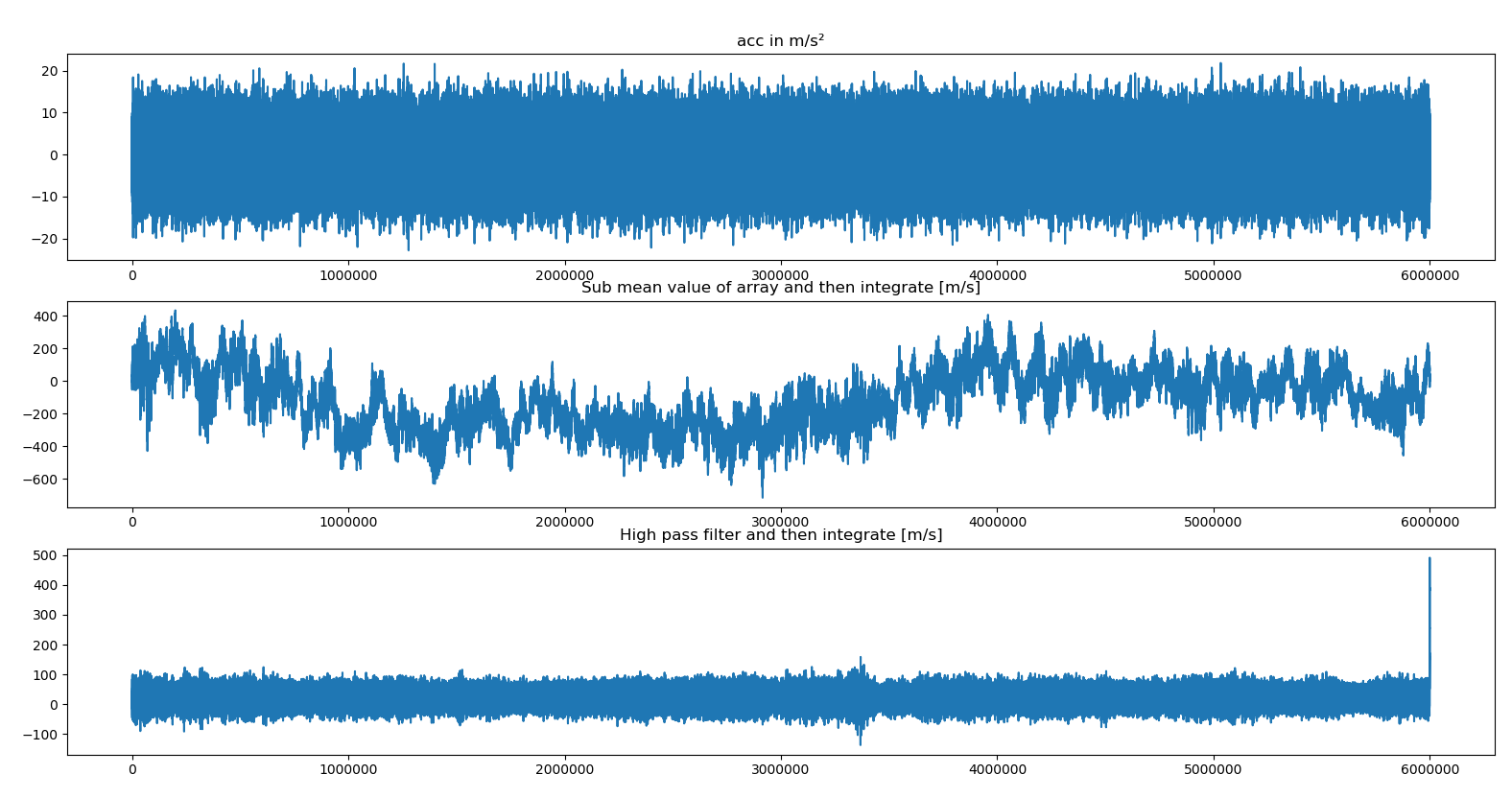
Code: Alles auswählen

def butter_highpass(cutoff, fs, order=2):
    nyq = 1 * fs
    normal_cutoff = cutoff / nyq
    b, a = signal.butter(order, normal_cutoff, btype='high', analog=False)
    return b, a

def butter_highpass_filter(data, cutoff, fs, order=2):
    b, a = butter_highpass(cutoff, fs, order=order)
    y = signal.filtfilt(b, a, data)
    return y


acc_mean =  acc.mean()
acc_subMean = acc-acc_mean

int_cumsum_subMean = np.cumsum(acc_subMean)

acc_hp = butter_highpass_filter(acc,10,1/dx)
int_cumsum_hp = np.cumsum(acc_hp)


fig, axs = plt.subplots(3)
axs[0].plot(channel['AccGen1Ax']['value_y'])
axs[0].set_title("acc in m/s²")

axs[1].plot(int_cumsum_subMean)
axs[1].set_title("Sub mean value of array and then integrate [m/s]")

axs[2].plot(int_cumsum_hp)
axs[2].set_title("High pass filter and then integrate [m/s]")

plt.show()

Kritik ist natürlich weiterhin willkommen!

Besten Dank und Gruß

Hallo zusammen,

ich bin noch recht unerfahren, habe mich aber an ein ähnliches Problem gewagt. Ich habe ein Beschleunigungssignal eines Schwingungssensors (16384 Daten innerhalb einer Sekunde). Folgende Programm habe ich geschrieben. Die fallende "Gerade" bei der Geschwindigkeit kann nicht sein. Denke mein Problem ist, dass ich den Werte von v0 nicht kenne und hier 0 eingesetzt habe, oder?

Code: Alles auswählen

import numpy as np
import matplotlib.pyplot as plt
csv = np.genfromtxt ('Schwingung.csv', delimiter=",")
time = csv[:,0]
acc = csv[:,1]
print(time)
print(acc)


plt.plot(time, acc)
plt.xlabel("Zeit")
plt.ylabel("Schwingung [mm/s^2]")
plt.show()


vel = [(((acc[0]+acc[1])/2)*(1/16383))+0]
l = len(time)
for i in range(l-2):
    vel.append((((acc[i+1]+acc[i+2])/2)*(1/16383))+vel[i])

vel.insert(0, 0)



plt.plot(time, vel)
plt.xlabel("Zeit")
plt.ylabel("Schwingung [mm/s]")
plt.show()

Kann mir hier wer weiterhelfen, wie ich das Problem lösen kann.

Danke.
Ben83

Da mE v0 nur ein Offset darstellt, und deine Formel kompliziert aber ok aussieht, würde ich die Daten sehen wollen.

Hallo. Das wären die Plots.

Beschleunigung (Rohsignal)
Bild

Geschwindigkeit:
Bild

PS: Warum werden die Bilder nicht angezeigt? Rechtsklick auf "BILD" zeigt aber den korrekten Link...

Weil es Links auf Webseiten und nicht Bilder sind. Ein klassisches Problem hier. Es wäre schön, wenn Bilder hier gehostet würden, aber das denke ich zu sehr ins Geld, das ohne Werbung aus privater Tasche kommt. Ist also so.

Wenn du v0 änderst, zb auf die Hälfte des erreichten Wertes der Integration, verändert sich dann die Steigung? Ich würde das erstmal überraschen, aber es ist ein Test deiner Hypothese.

Habe ich ausprobiert. Die Kurve wird nur um den neuen Startwert mehr oder weniger parallel verschoben.
v0 habe ich sowohl in der Formel geändert als auch bei der kompletiertung der Liste für t=0 (vel.insert(0, v0).

Was kann dann die Ursache sein? Wenn ich mir das Beschleunigungssignal anschaue, müsste doch auch das berechnete Geschwindigkeitssignal sowohl im positiven als auch im negativen Zahlenraum sein.

Squipy hat in diesen Beitrag ja von einer aufsteigenden Flanke gesprochen und drei Lösungsmöglichkeiten angegeben. Mit diesen kann ich leider nur nicht viel anfangen. Schon gar nicht wenn es um Filter geht.

viewtopic.php?f=30&t=46865#p355388

Ich habe tatsaechlich in diesem Moment das gleiche Problem - ich arbeite mit einer IMU um Vibrationen zu erfassen. Dazu benutze ich nicht deren Beschleunigung, sondern die Gyros. Und die haben bekannterweise Drift. Das sieht man hier ganz gut:

Bild

Oben sind die rohen Daten. Das Geraet wurde nicht bewegt, sondern liegt nur auf einem Lautsprecher, auf dem Musik gespielt wird. Wie man sieht dreht sich ueber die gesamten ~4-5 Minuten der Gyro langsam in eine Richtung. Die Vibrationen sind genauer gar nicht zu erkennen. Der harte Drop ist ein Knofpdruck, der den Wert auf 0 setzt.

Und darunter siehst du die Frequenzanteile mittels FFT aufgetragen. Zweimal, einmal mit scipy berechnet, einmal auf meinen Microcontroller (das ist das eigentliche Ziel). Wie man gut sieht, ist der Drop als Hochfrequenter Anteil in der FFT zu sehen. Was man auch sehen kann: am unteren Rand wird das Signal immer staerker, je weiter die Zeit fortschreitet. Das ist eben der tieffrequente Anteil, der sich durch diese Grade ausdrueckt.

Und jetzt die gleichen Daten, aber mit einem in der Frequenzdomaene super einfachen Hochpass-Filter, bei dem ich einfach die untersten 10 Baender abgeschnitten habe:

Bild

Und das meint Squipy auch mit seinen Loesungsmoeglichkeiten: man kann auf diese Weise einen Hochpass bauen, und aus den FFTs wieder das Signal synthetisieren. Damit sollte die Schraege verschwinden. Ich habe das noch nie probiert, und heute ist zu spaet. Aber das ist ein Weg. Es gibt aber auch andere Hochpass-Filter, und er benutzt einen. Last but not least kannst du auch einfach eine Gerade in deine Daten (die Geschwindigkeit!) fitten. Und aus der Steigung berechnest sich dadurch eine Beschleunigung, die im Schnitt eben diese Drift verursacht. Die kannst du dann einfach abziehen.

Das deutsche Python-Forum

Numerische Integration, a -> v

Numerische Integration, a -> v

Re: Numerische Integration, a -> v

Re: Numerische Integration, a -> v

Re: Numerische Integration, a -> v

Re: Numerische Integration, a -> v

Re: Numerische Integration, a -> v

Re: Numerische Integration, a -> v

Re: Numerische Integration, a -> v

Re: Numerische Integration, a -> v

Re: Numerische Integration, a -> v

Re: Numerische Integration, a -> v

Re: Numerische Integration, a -> v

Re: Numerische Integration, a -> v

Re: Numerische Integration, a -> v

Re: Numerische Integration, a -> v

Re: Numerische Integration, a -> v

Re: Numerische Integration, a -> v

Re: Numerische Integration, a -> v

Re: Numerische Integration, a -> v

Re: Numerische Integration, a -> v